This is some basic information about matrix transformation for people who forgot their math course or didn't have one.
Lets take that C = math.cos(A), S = math.sin(A), T = math.tan(A)
mtrx have to be used in the command ctx.transform(mtrx)
| Action | Command | Matrix for transform |
| Shift by dx,dy | ctx.translate(dx,dy) | mtrx = cairo.Matrix(1,0,0,1,dx,dy) |
| Scale by fx,fy | ctx.scale(fx,fy) | mtrx = cairo.Matrix(fx,0,0,fy,0,0) |
| Rotation to A radians | ctx.rotate(A) | mtrx = cairo.Matrix(C,S,-S,C,0,0) |
| Rotation to A radians with center in x,y | ctx.translate(x,y); ctx.rotate(A); ctx.translate(-x,-y) | mtrx = cairo.Matrix(C,S,-S,C,x-C*x+S*y,y-S*x-C*y) |
| X-skew by A | -- | mtrx = cairo.Matrix(1,0,T,1,0,0) |
| Y-skew by A | -- | mtrx = cairo.Matrix(1,T,0,1,0,0) |
| Flip H/V with center in cx:cy | -- | mtrx = cairo.Matrix(fx,0,0,fy,cx*(1-fx),cy*(fy-1)) |
| Flip H/V and rotation with center in cx:cy | -- | mtrx = cairo.Matrix(fx*C,fx*S,-S*fy,C*fy,C*cx*(1-fx)-S*cy*(fy-1)+cx-C*cx+S*cy,S*cx*(1-fx)+C*cy*(fy-1)+cy-S*cx-C*cy) |
(For flips fx/fy = 1 means 'no flip', fx/fy = -1 are used for horizontal/vertical flip).
To apply more than one transformation you can multiply matrix. 'Unfortunately' matrix multiplication is slightly different than regular multiplication of numbers. For square matrix with N columns and N rows the rule is 'Rij == sum of Aix to Bxj products, where x = [1,N]'. It's easy to figure out that for matrix multiplication A*B is not always the same as B*A. The rule of matrix multiplication is illustrated with a picture here:
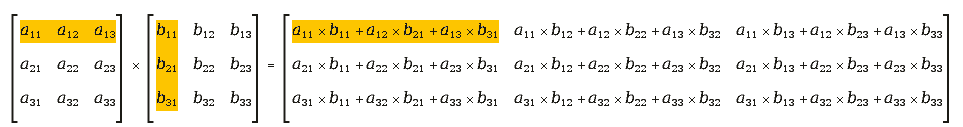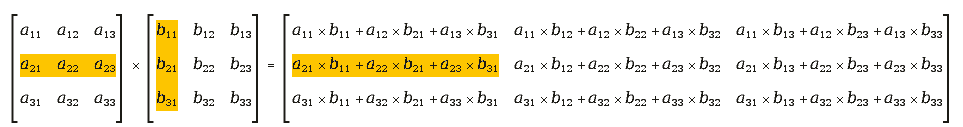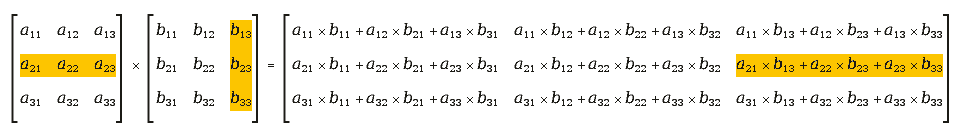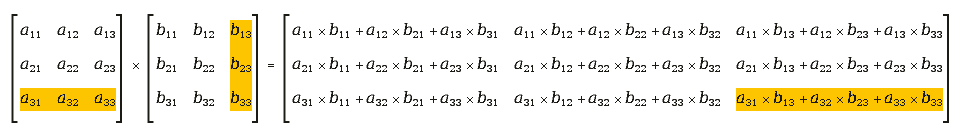
In a cairo.matrix(1,2,3,4,5,6), 1 is a11, 2 is a21, 3 is a12, 4 is a22, 5 is a13 and 6 is a23. a31 and a32 are 0, a33 is 1.
Cairo provides matrix multiplication and some other matrix functions.
